РІДИНА

1. Фазовий перехід газ - рідина.
2. Випаровування і конденсація.
3. Перегріта рідина і пересичений пар.
4. Поверхневий натяг.
5. Капілярні явища.

РІДИНА - одне з агрегатних станів речовини ( см. ГАЗ; ПЛАЗМА; ТВЕРДЕ ТІЛО ), Вона займає як би проміжне положення між кристалічним твердим тілом, що відрізняється повною впорядкованістю в розташуванні утворюють його частинок (іонів, атомів, молекул) і газом, молекули якого знаходяться в стані хаотичного (безладного) руху.

З рідким станом речовини людина зустрічається на кожному кроці. Перш за все, це звичайно вода , Незвичайна по ряду своїх властивостей рідина, так необхідна в повсякденному житті. Це і різні рідини неорганічного і органічного походження (кислоти, спирти, продукти переробки нафти і т.п.). Нарешті, це ртуть - дивовижна важка рідина блискучого кольору, схожа на розплавлений метал. При нагріванні до досить високих температур тверді тіла розплавляються і переходять в рідкий стан. Для кристалічних твердих тіл такий перехід відбувається стрибком при цілком певній для даного речовини температурі, званої температурою плавлення. Разом з тим, існують так звані аморфні (стеклообразниє) тверді тіла, які за своїми властивостями мало відрізняються від рідин, до їх числа відносяться скла, різні смоли, пластмаси. У міру підвищення температури вони переходять в рідкий стан - стають ніби все більш м'якими і набувають звичайну для рідини здатність текти. Їх називають іноді переохолодженими рідинами, оскільки в звичайному стані такі речовини можна розглядати як рідини з аномально великою в'язкістю.

При дуже низьких (в порівнянні з кімнатною) температурах в рідкий стан переходить більшість газів. Цей перехід також відбувається стрибком і характеризується для кожного газу своєю певною температурою переходу - температурою конденсації. Вся так звана кріогенна техніка заснована на отриманні та використанні рідкого гелію, рідкого азоту та інших зріджених газів.

На відміну від газу, одна з характерних особливостей рідини полягає в її здатності зберігати свій обсяг, що проявляється в її малої стисливості. Тверде тіло поряд зі збереженням обсягу прагне зберегти також і свою форму. Найбільш важлива відмінність рідини від твердого тіла полягає в тому, що вона приймає форму містить її судини, утворюючи при цьому вільну поверхню. Це означає, що рідина має високу плинністю (або малої в'язкістю). Гази через безладного характеру руху їх молекул прагнуть заповнити весь наданий їм об'єм.

Ці властивості рідини визначаються особливостями міжмолекулярної взаємодії в ній. Відомо, що в ідеальному газі молекули більшу частину часу проводять в стані вільного руху, взаємодіючи між собою лише в рідкісні моменти їх зближення. Середня відстань між ними можна визначити як r ~ n-1/3, де n - число часток в одиниці об'єму ( см. ГАЗ ). Для нормальних умов (тиск p = 1 атм., Температура T = 273 К) це відповідає відстані r ~ 3 · 10-7 см, що в 10 разів більше, ніж характерний діаметр самих молекул (d ~ 3 · 10-8 см) . У рідини молекули зближені один з одним, тобто відстані між ними виявляються того ж порядку величини, що й розміри молекул. Інтенсивна взаємодія між частинками рідини призводить до того, що їх рух вже не можна вважати повністю неврегульованим, як у випадку газового стану. Разом з тим, вони не досягають і того повного порядку в розташуванні молекул, яка характерна для кристалічних твердих тіл.

Як відомо, особливістю кристалічних твердих тіл є періодичність просторового розташування атомів, молекул або іонів, з яких складаються кристали. Сукупність таких періодично розташованих частинок утворює структуру, яка називається кристалічною решіткою. Подібна періодичність носить назву далекого порядку. Приклад двовимірного далекого порядку представлений на рис. 1а.

Експериментальні дослідження рідкого стану речовини, засновані на спостереженні дифракції рентгенівських променів і потоків нейтронів при проходженні їх через рідкі середовища, виявили наявність в рідині ближнього порядку, тобто наявність деякої впорядкованості в розташуванні частинок лише на малій відстані від будь-якої виділеної позиції. Це ілюструється картиною, зображеної на рис. 1б.

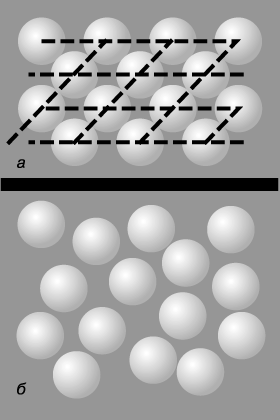
Розподіл часток в малій околиці будь-якої фіксованої частки рідини має певну впорядкованість, кілька нагадує кристалічну, хоча і більш рихлу. З цієї причини структуру рідини іноді називають квазікристалічної або кристалоподібні.

Вперше ідея про близькість деяких властивостей рідин (особливо розплавів металів) і кристалічних твердих тіл була висловлена ​​і потім розвивалася в роботах радянського фізика Я.І.Френкеля ще 1930-1940-х. Відповідно до поглядів Френкеля, який отримав тепер загальне визнання, тепловий рух атомів і молекул в рідині складається з нерегулярних коливань із середньою частотою, близькою до частоти коливань атомів в кристалічних тілах. Центр коливань визначається при цьому полем сил сусідніх частинок і зміщується разом із зсувами цих частинок. Спрощено можна уявити таке тепловий рух як накладення один на одного порівняно рідкісних перескоків частинок з одних тимчасових положень рівноваги в інші і теплових коливань в проміжках між стрибками. За образним висловом Я.І.Френкеля, молекули мандрують по всьому об'єму рідини, ведучи кочовий спосіб життя, при якому короткочасні переїзди змінюються відносно довгими періодами осілого життя. Середня тривалість коливань в стані тимчасового рівноваги сильно залежить від температури, тому підвищенням температури помітно збільшується рухливість молекул рідини і тим самим зменшується її в'язкість (або зростає плинність).

Через малу впорядкованості рідкого стану теорія рідини виявляється менш розвиненою, ніж теорія газів і кристалічних твердих тіл. Поки немає повної теорії рідини. На рівні існуючих теорій її структура, так само як і фізичні властивості, можуть бути описані на основі методів статистичної механіки з використанням різних функцій розподілу положень груп частинок. При цьому в більшості випадків досить знання невеликого числа функцій розподілу, з яких головне значення має так звана радіальна функція розподілу g (r), яка дає можливість виявлення будь-якої частки на відстані r від даної, обраної в якості точки відліку. Використання сучасних ЕОМ дозволяє розраховувати цю функцію методом комп'ютерного моделювання, грунтуючись на наявних даних про природу сил, що діють між молекулами. Порівняння функцій розподілу g (r), знайдених розрахунковим шляхом, з експериментальними, отриманими в результаті розшифровки рентгенограм (або нейтронограмм), дозволяє перевірити правильність припущень про природу міжмолекулярних сил і використовувати знайдені радіальні функції розподілу для визначення деяких властивостей рідин.

Особливий тип рідин - це деякі органічні сполуки, що складаються з молекул подовженою або дископодібної форми, або так звані рідкі кристали. Взаємодія між молекулами в таких рідинах прагне вибудувати довгі осі молекул в певному порядку. При високих температурах тепловий рух перешкоджає цьому, і речовина являє собою звичайну рідина. При температурах нижче критичної в рідини з'являється виділений напрям, виникає далекий орієнтаційний порядок. Зберігаючи основні риси рідини, наприклад, плинність, рідкі кристали мають характерні властивості твердих кристалів - анізотропією магнітних, електричних та оптичних властивостей. Ці їх властивості (поряд з плинністю) знаходять численні технічні застосування, наприклад в електронному годиннику, калькуляторах, мобільних телефонах, а також в моніторах персональних комп'ютерів, телевізорів, в якості індикаторів, табло та екранів для відображення цифрової, буквеної та аналогової інформації.

Фазовий перехід газ - рідина.

З досвіду відомо, що всі гази можна перевести в рідкий стан, якщо досить сильно їх стиснути або охолодити. При нормальних умовах (тиск p = 1 атм., Температура T = 273 К) газ можна вважати ідеальним, оскільки середня відстань між молекулами газу приблизно в 10 разів перевищує характерний розмір самої молекули. Якщо газ стискати, підтримуючи його температуру T постійної, то поки виконується умова ідеальності газу, зменшення обсягу газу V призводить до зростання тиску p відповідно до закону Клапейрона - Менделєєва, яке для одного благаючи газу записується у вигляді ( см. ГАЗ )

(1) pV = RT,

Якщо підвищити тиск до 100 атм., То молекули газу при цих умовах будуть в середньому віддалені один від одного на відстань, яке тільки вдвічі більше їх власних розмірів. При подальшому підвищенні тиску стає все більш істотним облік впливу сил міжмолекулярної взаємодії і власного обсягу молекул на поведінку газ. Рівняння стану реального (неідеального) газу вже не підкоряється закону (1). Одним з найбільш часто використовуваних напівемпіричних рівнянь стану є в цьому випадку рівняння Ван-дер-Ваальса

(2)

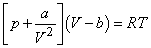
Поправка b враховує вплив власного обсягу молекул газу, а постійна a - вплив сил тяжіння між молекулами. хоча рівняння Ван-дер-Ваальса отримано для газів не дуже високої щільності, воно якісно правильно описує поведінку досить щільних газів і навіть перехід від газоподібного стану до рідкого.

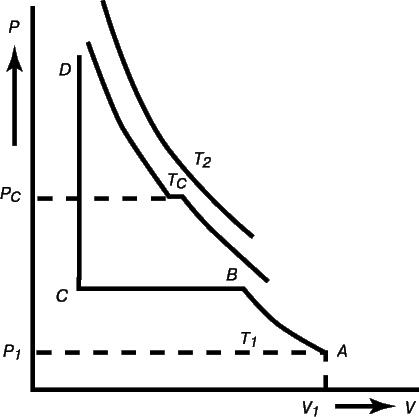
Мал. 2.

Гілки ізотерм для відносно великих значень обсягу або малих значень щільності відповідають газоподібному станом речовини. У цій області залежність тиску від об'єму підпорядковується рівнянню ідеального газу (1). Нехай початковий стан газу на одній з ізотерм зображується точкою. При ізотермічному стисканні газу точка, яка зображує його стан, буде переміщається вгору по обраної изотерме. Досвід показує, що, починаючи з певної точки A на изотерме, тиск в системі перестає підвищуватися, і процес подальшого стиснення описується ділянкою горизонтальної прямої AB. Фактично це означає, що, починаючи з цієї точки, система розпадається на дві фізично однорідні частини або фази: газоподібну і рідку. При русі вздовж прямої вліво кількість рідини зростає до тих пір, поки в точці B все речовина не перейде в рідкий стан. При подальшому зменшенні обсягу крива ізотерми від точки B різко йде вгору, що відповідає низькій стисливості утворилася рідини, при цьому більш високих температур системи відповідають все більш зменшуються горизонтальні ділянки ізотерм. В деякій точці C цю ділянку взагалі стягнеться в точку з координатами Tk і pk, які відповідають так званим критичної температури і критичному тиску. При T> Tk усоответствующіх ізотерм більше немає зламів.

На рис. 2 жирна колоколообразная крива, що з'єднує кінці горизонтальних ділянок ізотерм, ділить площину V - p діаграми на дві області. Область під цією кривою відповідає двофазному станом речовини - рівновага рідини і її пари. Область вище кривої відповідає однофаз станом речовини, в цій області втрачається якісна відмінність між рідиною і газом. Фактично це означає, що стискаючи газ можна перетворити його в рідину тільки тоді, коли його температура нижче критичної, але це не можна зробити ніяким підвищенням тиску, якщо температура газу вище критичної.

Наявність критичної точки ясно показує, що немає принципової різниці між рідким і газоподібним станом речовини. Можна розглянути будь-які два стани речовини, що відповідають двом точкам a і b на рис 2. Очевидно, менш щільний стан (a) відповідає газоподібному стану, а більш щільне (b) - рідини. Якщо стискати газ a при постійній температурі, то можна перетворити його в рідину b, слідуючи по одній з ізотерм і пройшовши при цьому стадію розшарування речовини на дві фази, але перейти від одного стану до іншого можна і іншим способом, якщо одночасно зі зменшенням обсягу спочатку збільшувати, а потім зменшувати температуру, пересуваючись в площині P, V уздовж будь-якого шляху, що обгинає критичну точку зверху (як це показано пунктиром на рис. 2). При цьому речовина всюди залишається однорідним і не можна сказати, де речовина перестало бути газом і стало рідиною.

Поведінка реальних ізотерм, представлених на рис. 2, якісно вірно передається рівнянням Ван-дер-Ваальса (2). На рис. 3 представлені дві такі ізотерми, одна з яких має точку перегину, відповідну критичних значень T k і pk, а інша, що лежить нижче, містить хвилеподібний ділянку BDEFA. Такий вид ізотерми є графічним зображенням рівняння третього ступеня щодо величини V, до якого наводиться рівняння (2).

Мал. 3

У порівнянні з досвідченою изотермой ізотерма Ван-дер-Ваальса замість горизонтальної ділянки має в цій області характерний завиток з максимумом і мінімумом. Це означає, що не всі стани речовини, сумісні з хвилеподібним ділянкою кривої Ван-дер-Ваальса, можуть бути реалізовані в дійсності. Зокрема, ділянка DF, де тиск зростає зі збільшенням обсягу, суперечить умові термодинамічної стійкості речовини. Іншими словами, при зростанні обсягу V все ізотерми повинні монотонно спускатися, що і спостерігається на практиці. Разом з тим при особливих умовах можуть бути реалізовані стану, зображувані ділянками ізотерми BD і FA. Ці стани називаються метастабільними.

Випаровування і конденсація.

У всій області зміни параметрів по ходу прямої ділянки ізотерми Ван-дер-Ваальса існує термодинамічна рівновага межу рідиною і газом. Це означає, що швидкість випаровування (число молекул, що залишають одиницю поверхні рідини в 1 с) дорівнює швидкості конденсації пари (числу молекул пара, які повертаються в рідину). Рівновага з парою, який в такому випадку називається насиченим, встановлюється само собою, якщо рідина знаходиться в закритій посудині.

Процес встановлення такої рівноваги можна представити таким чином. Пар над поверхнею рідини утворюється в результаті вильоту частини молекул з її поверхні. Для виходу з рідини випаровуються молекули повинні подолати сили тяжіння з боку решти молекул, тобто зробити роботу проти цих сил. Крім того, повинна бути здійснена робота проти зовнішнього тиску вже утворився пара. Очевидно, вся ця робота може бути здійснена за рахунок кінетичної енергії теплового руху молекул. Природно, що не всі молекули здатні зробити цю роботу, а тільки ті з них, які мають достатню для цього кінетичної енергією, тому перехід частини молекул в пар призводить до збіднення рідини швидкими молекулами, тобто до її охолодження. Відчуття сильного охолодження шкіри, змоченою, наприклад, ефіром (швидко випаровується рідиною) є наслідком цього ефекту.

Щоб швидкість випаровування рідини лишалася незмінною і навіть зростала, потрібно підтримувати незмінною температуру її поверхні, що забезпечується постійним підведенням тепла від зовнішнього джерела. Одночасно з переходом молекул з об'єму рідини в газову фазу відбувається і зворотний процес: повернення частини молекул в рідину (конденсація). Очевидно, число конденсуються молекул пропорційно щільності молекул в парі, тому в замкнутому посудині через деякий час, коли швидкості прямого і зворотного процесів зрівняються, настає рівновага. Встановлена ​​таким чином постійна щільність пара відповідає цілком певному тиску, яке називається пружністю насиченої пари, яка росте з підвищенням температури.

Перехід Речовини з однієї фази в іншу всегда пов'язаний з поглінанням або віділенням деякої кількості тепла - так званої пріхованої теплоти фазового переходу (або просто теплотою переходу). Кількість тепла, необхідне для того, щоб випаровуваності Рідини з поверхні відбувалося при Постійній температурі (при зовнішньому тиску, рівному пружності ее насіченої парі), назівається теплотою випаровуваності, яка віявляється універсальною характеристикою кожної Рідини. Зворотнього випаровуваності процес конденсації супроводжується віділенням тепла. При цьом очевидно, теплота конденсації дорівнює теплоті випаровуваності. Теплота переходу є Фактично кількісною характеристикою сил зв'язку между молекулами Речовини - чим более ЦІ сили, тім более теплота переходу. Стосовно до рідини можна сказати, що потенційна енергія молекули в рідині менше її потенційної енергії в парі на величину, рівну теплоті випаровування, віднесеної до однієї молекулі. На практиці користуються питомою теплотою випаровування (конденсації), яка виходить розподілом молярної (віднесеної до одного молю) теплоти випаровування до молекулярної масі рідини.

Кипіння рідини - процес її випаровування, що супроводжується швидким утворенням і зростанням бульбашок пари, які прориваються через поверхню рідини назовні. Якщо рідина в посудині нагрівати при постійному зовнішньому тиску, то спочатку освіту пара носить спокійний характер, оскільки випаровування відбувається тільки з вільної поверхні рідини, однак, при досягненні певної температури, званої температурою кипіння, освіту пара починає відбуватися не тільки з вільної поверхні, але і зсередини рідини.

У реальності, в самій рідини або на стінках посудини, в який вона укладена, завжди є розчинений (або адсорбований на стінках) повітря або будь-якої іншої газ. В цьому випадку при нагріванні рідини в ній утворюються бульбашки повітря, які наповнюються насиченим паром навколишнього рідини. У стані механічної рівноваги сума тисків повітря і пара усередині бульбашки повинна дорівнювати зовнішньому тиску поза бульбашки, яке складається з тиску атмосфери і гідростатичного тиску навколишнього рідини. З підвищенням температури рідини внутрішній тиск в бульбашках зростає, вони починають збільшуватися в розмірах і підніматися вгору під дією архимедовой підйомної сили. Така двухфазная система (рідина з повітряними бульбашками) виявляється нестійкою і починається бурхливий процес кипіння.

Температура кипіння відповідає умові, при якому тиск насиченої пари дорівнює сумі атмосферного і гідростатичного тиску на даній висоті, звідки випливає, зокрема, що температура кипіння рідини істотно залежить від зовнішнього тиску. Якщо помістити посудину з водою під ковпак повітряного насоса, то при відкачці повітря до певного тиску можна змусити воду кипіти при кімнатній температурі. З цим же пов'язане спостережуване зниження температури кипіння рідин при підйомі в горах на великі висоти, де атмосферний тиск повітря помітно нижче тиску біля підніжжя. Так, температура кипіння води на висоті 4000 м складає лише 85 ° C в порівнянні з температурою кипіння 100 ° C на рівні моря.

Перегріта рідина і пересичений пар.

Кипіння може відбуватися лише в тому випадку, коли рідина містить розчинені в ній гази. При відсутності газових бульбашок або центрів інтенсивного пароутворення можна отримати перегріту рідину, тобто рідина, температура якої вище температури кипіння при даному зовнішньому тиску, але яка, однак, не закипає. На изотерме Ван-дер-Ваальса (рис. 3) перегріта рідина відповідає ділянці BD, так як тиск рідини на цій ділянці нижче тиску на изотерме-ізобарі AB, де воно дорівнює тиску насиченої пари. Перегріту рідину можна отримати навіть тоді, коли в ній є бульбашки, треба лише, щоб вони були досить малі, так що тиск насиченої пари всередині них виявляється помітно меншим відповідного тиску пара над плоскою поверхнею. При малих розмірах бульбашки важливо і тиск на пухирець, пов'язане з кривизною його поверхні. Сферична поверхню рідини, що оточує бульбашку, за рахунок поверхневого натягу прагне скоротитися і виникає при цьому тиск додається до зовнішнього тиску, розчавлює бульбашка.

Перегріта рідина метастабильна, тобто мало стійка. При наявності зародків (наприклад, досить великих бульбашок повітря) рідина вже не може існувати як фізично однорідне тіло і частина її негайно переходить в пар.

Так само йде справа з пересиченим паром. На изотерме Ван-дер-Ваальса йому відповідає ділянку FA (рис. 3). Якщо в пересиченому парі утворилися зародки нової фази (наприклад, великі крапельки рідини), то за певних умов, коли рівноважний тиск пари над поверхнею крапельки менше тиску навколишнього пересичені пара, пара конденсується. Конденсації пересичені пара сприяє і наявність пилу або інших дрібних частинок. Ефективними центрами конденсації виявляються електрично заряджені частинки або іони. Цей ефект лежить в основі дії одного з основних приладів ядерної фізики і фізики елементарних частинок - камери Вільсона.

Камера Вільсона є герметично замкнутий обсяг, заповнений якимись неконденсірующаяся газом (гелій, аргон та ін.) І насиченими парами деяких рідин (вода, етиловий спирт і ін.). Одна зі стінок камери робиться рухомого (у вигляді поршня або пружною діафрагми). При адіабатичному розширенні температура суміші, що заповнює камеру, знижується. При цьому пар стає пересиченим, але без центрів конденсації конденсуватися не буде. Якщо, проте, через простір камери пролетить зарядженачастка, вона залишить за собою ланцюжок іонів. На цих іонах, як на зародках, відразу починається конденсація пересичені пара у вигляді маленьких крапельок, що досягають видимих ​​розмірів. Так виникають треки - ланцюжки крапельок, розташованих уздовж траєкторії іонізующей частки, які можна висвітлити і сфотографувати.

Для спостереження слідів іонізуючих частинок можна використовувати і явища в перегрітій рідині, на цьому заснована дія так званої бульбашкового камери, яка з'явилася набагато пізніше камери Вільсона. Рідина в бульбашкової камері (рідкий водень, рідкий гелій, рідкий пропан, фреони та ін.) Знаходиться при температурі, що перевищує температуру кипіння. Від закипання вона утримується високим тиском над нею. При раптовому зниженні тиску рідина виявляється перегрітої. Якщо в цей момент через камеру пролітає іонізующих часток, то у вузькій області уздовж її траєкторії рідина закипає. В результаті шлях частинки виявляється зазначеним ланцюжком бульбашок пари, яку можна зафіксувати.

Затвердіння (кристалізація) рідин - перетворення рідини в тверде тіло (затвердіння або кристалізація) є прикладом іншого фазового переходу. Цей перехід відбувається при певній температурі (температурі затвердіння) і супроводжується виділенням тепла (теплоти затвердіння). Навпаки, при плавленні твердого тіла (переході його в рідкий стан) необхідна витрата деякої кількості тепла (теплота плавлення). Очевидно, теплота плавлення повинна бути дорівнює теплоті затвердіння.

Як і у випадку з перенасиченим паром, який переходить в рідину при наявності центрів конденсації, можливі стану, відповідні переохолодженої рідини, тобто рідини, охолодженою до температури нижче температури затвердіння. Така рідина зазвичай дуже швидко кристалізується при появі в ній сторонніх вкраплень, здатних виконувати функції зародків кристалічної фази. Існують, однак, переохолоджені рідини, в яких швидкість кристалізації дуже мала. До них відносяться, наприклад, мед і варення, які «засахариваются» лише після закінчення довгого часу. Багато тіл, які в побуті називають твердими, не володіють кристалічною структурою, і їх правильніше розглядати як переохолоджені рідини (скло, асфальт, шевський вар, деякі смоли і ін.). У склі, наприклад, переохолодження настільки сильне, що практично немає ні освіти зародків, ні кристалізації на існуючих зародках. Разом з тим, дуже повільний процес кристалізації йде і тут. Він призводить до того, що після закінчення десятків років скло може стати каламутним ( «расстекловиваніе» скла).

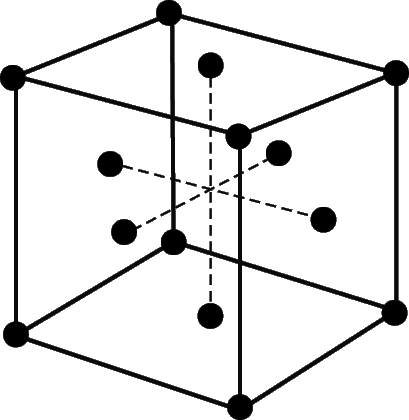
Зазвичай при розплавленні твердого тіла обсяг його збільшується приблизно на 10%, тобто середня відстань між сусідніми частинками (молекулами або іонами) в твердому і рідкому станах майже однаково. Відповідно при затвердінні рідин їх обсяг дещо зменшується, хоча є й винятки з цього правила. Наприклад, вода, галій та вісмут при затвердінні розширюються, так що затверділе речовина плаває на поверхні рідини. Поблизу температури затвердіння можливі і інші аномалії в поведінці рідин. Так, звичайна вода при підвищенні температури від 0 до 4 ° C стискається. Рентгеноструктурні дослідження типових твердих тіл кристалічної структури показують, що при переході їх в рідкий стан далекий порядок порушується, але якийсь ближній порядок залишається. Алюміній, наприклад, кристалізується з утворенням гранецентрированной кубічної решітки (рис. 4), в якій кожен атом оточений дванадцятьма найближчими сусідами, розташованими на відстані 2,86 А (2,86 · 10-8 см). У рідкому алюмінії кожен атом оточений 10-11 найближчими сусідами, розташованими на відстані 2,96 А від нього. Структура таких рідин поблизу температури затвердіння подібна до структури кристалічного твердого тіла, проте, виявляється дещо «пухкої». Виявляється, що для води, галію і вісмуту спостерігається зворотна картина: більш «пухкою» поблизу температури затвердіння є їх структура не в рідкому, а в твердому стані. Причину таких аномалій слід шукати в особливостях будови молекул різних речовин і зв'язків між ними в різних агрегатних станах.

Поверхневий натяг.

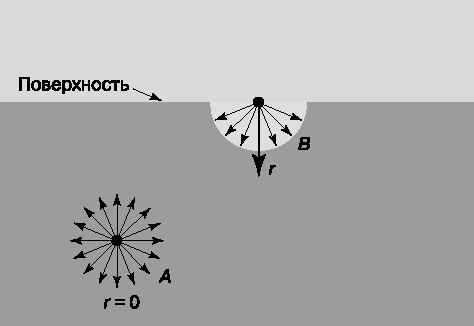
Деякі властивості рідин пов'язані з наявністю у них вільної поверхні. Тут, так само, як і в випадку об'ємних явищ в рідини, виявляється дія сил міжмолекулярної взаємодії. Природа ефекту поверхневого натягу. стане ясніше з розгляду рис. 5. Тут A і B - дві молекули рідини, одна в обсязі, інша на поверхні. В обох випадках на них діють сили тяжіння з боку інших молекул, але лише тих, які знаходяться всередині сфери діаметром в декілька ангстрем, оскільки ці сили швидко зменшуються з відстанню. Для молекули A така сфера повністю лежить всередині рідини, тому рівнодіюча всіх сил дорівнює нулю. Молекула B, що знаходиться на поверхні, буде втягуватися всередину рідини, оскільки на неї діють тільки сили тяжіння з боку молекул, що знаходяться в нижній півсфері. Такі ж сили, перпендикулярні поверхні і спрямовані всередину рідини, діють на всі молекули поблизу поверхні; вони і створюють поверхневий натяг.

Поверхневий натяг S кількісно визначається як сила, що діє на одиницю довжини лінії на поверхні рідини. Нехай є мильна плівка, натягнута на вертикальну рамку з двох тонких зволікань TUV і PQ (рис. 6). Зволікання PQ не закріплена і може вільно пересуватися.

Перехід молекули з глибини рідини в поверхневий шар пов'язаний з необхідністю здійснення роботи проти діючих в поверхневому шарі сил. Ця робота, що здійснюються молекулою за рахунок запасу її кінетичної енергії, йде на збільшення потенційної енергії молекули. Ситуація тут подібна розглянутій в механіці, коли тіло кинуто вгору тілом і робота, що здійснюються летять тілом проти сил земного тяжіння, йде на збільшення потенційної енергії тіла. Таким чином, молекули в поверхневому шарі володіють додатковою потенційною енергією (поверхневою енергією). Очевидно, поверхнева енергія пропорційна площі поверхні розділу

U пов. = A S (3)

Коефіцієнт a називається коефіцієнтом поверхневого натягу або просто поверхневий натяг

Поверхневий натяг можна кількісно визначити як силу, що діє на одиницю довжини лінії на поверхні рідини. Це можна розглянути на прикладі тієї ж прямокутної дротяної рамки з рухомою перемичкою, затягнутою плівкою рідини (рис. 6). Плівка подвійна, складається з двох простих плівок, між якими знаходиться рідина. Через наявність поверхневої енергії плівка прагне скоротити свою поверхню, перемичка починає рухатися вгору під дією сили, яка дорівнює 2 a l, де l - довжина перемички. Для утримання в рівновазі перемички до неї треба докласти певну силу 2 F (з урахуванням присутності двох плівок).

Мал. 6

Нехай перемичка перемістилася в напрямку дії сили F на дуже малу величину D x, при цьому над плівкою здійснена робота D A = 2 F D x = 2a l D x. Оскільки площа плівки при такому переміщенні збільшиться на D s = 2a l D x, вироблена над плівкою робота визначається як D A = aD S. Ця величина відповідає збільшенню поверхневої енергії рідини, і відповідно до формули (3) введений вище коефіцієнт a дійсно є коефіцієнт поверхневого натягу, який можна визначити з співвідношення

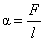(4)

З механіки відомо, що, положення рівноваги тіла або системи тіл відповідає мінімуму потенційної енергії системи, тому рідина, надана сама собі, приймає форму з мінімальною поверхнею, тобто форму кулі. Таку форму кулястої краплі (незалежно від її розмірів) набуває рідина в невагомості, що неодноразово спостерігалося під час польотів космічних кораблів. У земних умовах рідина приймає форму, відповідну мінімуму сумарної енергії - енергії в полі земного тяжіння і поверхневої енергії. Оскільки перша пропорційна обсягу тіла, а друга - поверхні, відносний вплив сили тяжіння тим більше, чим більший об'єм краплі, тому малі краплі води (і особливо ртуті) виявляються практично кулястими. Великі краплі сплющуються під дією сил тяжіння. У земних умовах можна повністю виключити вплив сили тяжіння, зануривши деяку масу рідини в посудину з іншою рідиною, яка не змішується з першою. Щільності обох рідин повинні бути при цьому однакові. Такий досвід був вперше поставлений Плато, який взяв суміш спирту і води і помістив в неї велику краплю оливкової олії. Щільності рідин були підібрані однаковими, і оливкова олія прийняло форму кулі.

Проявом сил поверхневого натягу є і динаміка відриву крапель при її стікання з будь-якої поверхні (або випливають з вузької трубки) під дією сил тяжіння. Висить крапля нагадує рідину, підвішену в гумовому мішечку. Однак натяг гумової плівки змінюється зі зміною кількості укладеної в ній рідини, а поверхневий натяг від розмірів краплі не залежить. Це дозволяє пояснити явище відриву крапель. Коли крапля досягає певного розміру, на ній утворюється шийка (звуження), яка стає все тоншою в міру збільшення розмірів краплі. У певний момент на шийці матки виникає друге звуження, і, нарешті, крапля розривається відразу в двох місцях. В результаті, коли відривається велика крапля, за нею завжди йде мала крапелька (кульку Плато).

Капілярні явища.

Своєрідні явища відбуваються на кордоні двох змішуються рідин, або рідини і твердого тіла. Форма, яку приймає рідина в зіткненні з твердим тілом, визначається співвідношенням трьох, що діють на рідину сил: сили тяжіння, сил взаємодії молекул рідини і сил взаємодії між частинками рідини і частинками твердого тіла, з яким вона контактує. Це відповідає різним значенням так званого крайового кута, тобто кута, утвореного дотичною до поверхні рідини у її кордону з твердим тілом і поверхнею самого твердого тела.Так, крапля води на чистій скляній платівці втрачає свою сферичну форму і розтікається, утворюючи тонку плівку, відбувається це тому, що сили зчеплення між молекулами води і скла істотно перевищують аналогічні сили між молекулами води. Крайовий кут в цьому випадку близький до нуля, а явище розтікання рідини носить назву повного змочування. Навпаки, крапля ртуті на тій же платівці залишається сферичної, крайовий кут в цьому випадку близький до 180o, що відповідає випадку повного несмачіванія.

Если велика Кількість Рідини налито в широкий посудину, то форма ее поверхні візначається силою тяжіння, яка Забезпечує плоску горизонтальну поверхню. Однако у самих стінок Посудини поверхню Рідини віявляється вікрівленою, утворюється меніск, увігнутій у змочуючіх рідін и опуклій - у несмачіваеміх. Можна показати, що кривизна поверхні рідини призводить до появи додаткових сил, що діють на рідину під цією поверхнею. Величина цього додаткового тиску в разі сферичної поверхні радіуса 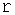визначається відомою формулою Лапласа

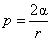(5)

У разі опуклої поверхні додатковий тиск направлено всередину рідини, тобто додається до нормального тиску рідини. У разі увігнутої поверхні рідина буде перебувати під меншим тиском, ніж та ж рідина під плоскою поверхнею.

Якщо рідина знаходиться у вузькій трубці (капілярі), вплив стінок простягається на всю поверхню рідини і вона утворює меніск на всьому своєму протязі. Очевидно, це має місце в тому випадку, коли радіус трубки порівняємо з радіусом кривизни поверхні рідини на кордоні з твердим тілом. У таких трубках спостерігаються явища, які отримали назву капілярних явищ. На рис. 7 і 7а зображена вузька трубка, опущена в широкий посудину з рідиною.

Нехай стінки трубки змочуються рідиною (наприклад, вода і скло - рис. 7). Тоді вода, що проникла в трубку, утворює увігнутий меніск. Внаслідок тиску, викликаного кривизною поверхні рідини, вода всередині капіляра відчуває тиск p, спрямоване до центру кривизни меніска, тобто на гору. Під дією цього тиску рідина піднімається по трубці до рівня h, при якому гідростатичний тиск r gh стовпа води висотою h, врівноважує тиск p.

Умова рівноваги має при цьому вид

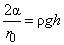, (6)

де r 0 - радіус меніска. Це рівність визначає висоту підйому рідини в капілярі.

Якщо крайовий кут рідини, яке стикається із стінками капіляра дорівнює q, то

r 0 = r / cos q, де r - радіус капіляра. В цьому випадку висота підйому рідини в капілярі визначається як

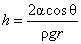(7)

Капілярним підйомом пояснюється ряд широко відомих явищ: вбирання рідини фільтрувальної папером, рух гасу або масла уздовж гніту. Капілярні сили забезпечують і харчування грунтової водою стовбурів і крон дерев. У всіх цих випадках волокна відповідних матеріалів і деревина грають роль дуже тонких капілярів.

Якщо рідина не змочує капіляр, картина буде протилежною, так як меніск в цьому випадку опуклий і тиск Лапласа направлено вниз. Рівень рідини в капілярі буде тепер нижче її рівня в посудині. Найпростішим прикладом служить приміщення вузької трубки в посудину з ртуттю (рис. 7а). Формула (7) виявляється як і раніше справедливою. Значення крайового кута q, що лежать між 90 і 180 градусами, дають негативні значення h, що і відповідає рівню, який лежить нижче рівня рідини в широкому посудині.

Володимир Жданов